🔢 Calculadora de Sumas Binario – ¡Realiza tus Cálculos Binarios al Instante! ⚡
¿Listo para sumar en binario sin complicaciones? 🧮 Nuestra calculadora online es rápida, precisa y perfecta para estudiantes, programadores y amantes de la tecnología. 🚀
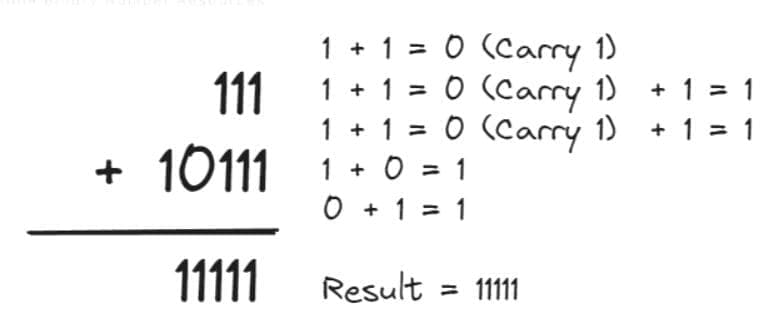
| A | B | A + B | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 10 | 0 | 10 | 0 |
| 10 | 1 | 11 | 0 |
| 11 | 0 | 11 | 0 |
| 11 | 1 | 100 | 1 |
| 100 | 0 | 100 | 0 |
| 100 | 1 | 101 | 0 |
| 101 | 0 | 101 | 0 |
| 101 | 1 | 110 | 0 |
| 110 | 0 | 110 | 0 |
| 110 | 1 | 111 | 0 |
| 111 | 0 | 111 | 0 |
| 111 | 1 | 1000 | 1 |
¿Es posible realizar sumas en el sistema binario de manera sencilla? Sí. Gracias al Calculador de Suma Binaria, sumar números representados por ceros y unos nunca ha sido tan fácil. En un mundo donde la tecnología avanza a pasos agigantados, entender el lenguaje de las computadoras es más relevante que nunca.
La suma binaria puede parecer complicada al principio, pero con las herramientas adecuadas y un poco de práctica, se convierte en una habilidad accesible para todos.
Aquí te mostramos por qué este calculador es una herramienta imprescindible:
- Facilidad de Uso: Solo necesitas ingresar tus números binarios y el calculador hará el resto.
- Rapidez: Obtén resultados instantáneos sin complicaciones ni cálculos manuales.
- Versatilidad: Además de sumar, puedes restar, multiplicar y dividir números binarios con la misma herramienta.
- Precisión: Olvídate de los errores humanos; el calculador ofrece resultados exactos cada vez.
Comprender las reglas básicas de la suma binaria es esencial para cualquier entusiasta del mundo digital. Estas reglas son simples y directas: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1 y 1 + 1 = 10 (donde llevamos uno al siguiente dígito). Con estas bases claras, no solo podrás sumar números binarios manualmente si lo deseas, sino también apreciar cómo esta operación fundamental impacta en técnicas avanzadas como la corrección y detección de errores en datos digitales. ¡Descubre más sobre cómo dominar este fascinante aspecto del cálculo digital!
¿Qué es el sistema binario?
El sistema binario es un sistema numérico de base 2 que utiliza solo dos símbolos: 0 y 1. Cada dígito en este sistema se denomina bit. Este sistema es fundamental en las aplicaciones informáticas, ya que los números binarios representan datos internamente a través de circuitos electrónicos que utilizan compuertas lógicas. Por ejemplo, el número decimal 4 se representa como (100)₂ en binario.
A diferencia del sistema decimal, que opera en base 10 con dígitos que van del 0 al 9, el sistema binario usa estrictamente los dígitos 0 y 1. Este sistema es crucial para los lenguajes de programación como C, C++ y Java, permitiendo a las computadoras codificar y procesar información digital de manera eficiente.
¿Cómo usar la calculadora de suma binaria?
Usar una calculadora de suma binaria es sencillo. Primero, debes ingresar dos valores binarios en los campos designados. La calculadora realizará la suma basada en las reglas del binario, donde el acarreo ocurre cuando la suma equivale a 2 (binario) en lugar de 10 (decimal).
Ten cuidado con errores comunes, como interpretar 1 + 1 = 0 con un acarreo de 1. Los dígitos acarreados pueden afectar las columnas subsiguientes. Además, recuerda que los ceros a la izquierda son significativos en los cálculos binarios y no deben omitirse, ya que impactan el resultado final.
¿Cuáles son las reglas de la suma binaria?
La suma binaria sigue principios similares a la suma decimal, comenzando desde el dígito más a la derecha y moviéndose hacia la izquierda a través de los valores de lugar (unos, doses, cuatros, etc.).
El reagrupe ocurre cuando la suma de dos dígitos supera 1, a diferencia del reagrupe decimal que ocurre en sumas superiores a 9. Las posibles salidas al sumar dos dígitos binarios son:
- 0 + 0 = 0 (sin acarreo)
- 0 + 1 = 1 (sin acarreo)
- 1 + 0 = 1 (sin acarreo)
- 1 + 1 = 0 con un acarreo de 1 a la siguiente columna
Por ejemplo, sumar (101)₂ y (10)₂ resulta en (111)₂ sin acarrear dígitos más allá de uno. Sin embargo, sumar (1001)₂ y (111)₂ resulta en una suma de (11000)₂ debido al acarreo de múltiples columnas. Al sumar números binarios negativos, primero debes representarlos en un formato de bits fijo, encontrar su complemento a uno, sumarlos incluyendo cualquier acarreo final, y luego encontrar el complemento a uno del resultado para obtener una respuesta negativa final.
Suma binaria: Sumar números binarios
Para sumar números binarios, coloca los números verticalmente, alineando los dígitos por valor de lugar (unos, doses, cuatros, etc.). Comienza sumando desde el dígito más a la derecha (lugar de los unos). Las sumas posibles son:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (acarreo de '1' a la siguiente columna)
Si ambos dígitos son '1', escribe '0' y acarrea '1'. Si hay un acarreo de la columna anterior, inclúyelo en tu suma para esa columna. Continúa este proceso para cada columna hasta que todas hayan sido sumadas. Por ejemplo: Sumar los números binarios 0111 (7 en decimal) y 1110 (14 en decimal) da como resultado '10101', que equivale al número decimal '21'.
Beneficios de usar una calculadora de suma binaria
Una calculadora de suma binaria ofrece varias ventajas:
- Simplificación de operaciones complejas: Hace que las operaciones aritméticas binarias como la suma, resta, multiplicación y división sean sencillas, incluso para números grandes.
- Cálculos firmados y no firmados: Puede manejar representaciones binarias tanto firmadas como no firmadas, crucial para cálculos precisos.
- Soporte de conversión: Facilita la conversión entre sistemas binarios y decimales, mejorando la comprensión y manipulación de números.
- Reducción de errores: Al automatizar los cálculos, minimiza el riesgo de errores humanos comunes en la aritmética binaria manual.
- Claridad en operaciones a nivel de bit: Permite realizar operaciones avanzadas como desplazamientos de bits y lógicas AND, OR y XOR fácilmente.
- Mejora del aprendizaje: Sirve como una ayuda didáctica para ayudar a los usuarios a comprender las reglas de la suma binaria a través de ejemplos prácticos.
Errores Comunes en la Suma Binaria y Cómo Evitarlos
Al realizar sumas binarias, es fácil cometer errores. Uno de los más comunes es confundir las reglas binarias con las decimales, lo que lleva a resultados incorrectos.
Otro error frecuente es olvidar el acarreo: como en la suma decimal, no recordar acarrear cuando la suma supera 1 (por ejemplo, 1 + 1 = 10). También hay errores al sumar incorrectamente los bits, especialmente en operaciones de múltiples bits. Además, algunos pueden ignorar los valores de lugar en binario, lo que puede llevar a desalineaciones y errores en la suma.
Preguntas Frecuentes
¿Qué es la suma binaria?
La suma binaria es la operación de sumar números en forma binaria. Funciona de manera similar a la suma decimal, pero solo usa 0's y 1's como dígitos. Cuando la suma excede 1, debes acarrear 1 al siguiente bit. Por ejemplo, 101 + 101 = 1010.
¿Cómo resolver la suma binaria?
Para resolver la suma binaria, realiza una suma larga: coloca los números verticalmente y suma los dígitos en columnas de derecha a izquierda. Si la suma en una columna es igual a 2, acarrea 1 a la siguiente columna (a la izquierda). Si la suma es 1 o 0, escríbela y pasa a la siguiente columna. Procede de esta manera hasta sumar todas las columnas (incluyendo los números acarreados).
¿Cómo detectar un desbordamiento en la suma binaria?
El desbordamiento en la suma binaria ocurre cuando el resultado de sumar dos números en complemento a 2 de N bits excede el rango representable. Ocurre si dos números positivos dan un resultado negativo o si dos números negativos dan un resultado positivo. Se identifica comparando el acarreo de entrada (C-in) y el acarreo de salida (C-out) del bit más significativo (MSB): si C-in ≠ C-out, ha ocurrido un desbordamiento. Por ejemplo, sumar 7 (0111) y 1 (0001) en un sistema de 4 bits resulta en un valor fuera de rango (1000), indicando desbordamiento ya que representa -8 en lugar de 8.
| Operación | Resultado Binario | Resultado Decimal |
|---|---|---|
| 101 + 110 | 1011 | 11 |
| 1110 + 1011 | 11001 | 25 |
| 1001 + 111 | 10000 | 16 |
Conclusion
El Calculador de Suma Binaria es una herramienta esencial para cualquier persona interesada en el mundo digital. Con su facilidad de uso, rapidez y precisión, transforma lo que podría ser un proceso complejo en una tarea simple y accesible. Este calculador no solo permite realizar sumas binarias con facilidad, sino que también ofrece la capacidad de restar, multiplicar y dividir números binarios, brindando una versatilidad impresionante.
La suma binaria sigue reglas básicas que pueden parecer desafiantes al principio, pero con práctica se vuelven intuitivas: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1 y 1 + 1 = 10 (donde llevamos uno al siguiente dígito). Al comprender estas reglas fundamentales, los usuarios no solo pueden realizar cálculos manualmente si lo desean, sino también apreciar la importancia de esta operación en técnicas avanzadas como la corrección de errores.
Además, el sistema binario es la base sobre la cual funcionan las computadoras modernas. Comprenderlo es crucial para quienes buscan adentrarse más en el ámbito tecnológico. En resumen, el Calculador de Suma Binaria no solo simplifica las operaciones matemáticas sino que también abre las puertas a un mayor entendimiento del lenguaje informático básico.