💻⚙️ Conversor de Fracciones Binarias: ¡Transforma Binario en Decimal al Instante! 🧮
¿Necesitas convertir fracciones binarias a decimal y viceversa? 🎯 Nuestro conversor online te facilita el trabajo con precisión y rapidez, ¡ideal para estudiantes y amantes de la tecnología! 🚀
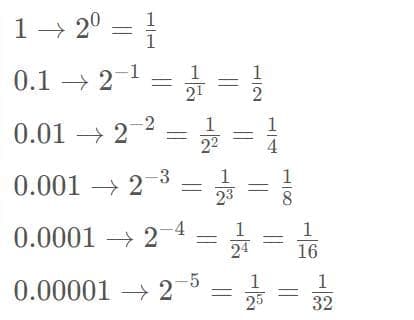
¿Alguna vez te has preguntado cómo los ordenadores entienden y procesan números que no son enteros? Si la respuesta es sí, entonces el mundo de las fracciones binarias es un terreno fascinante por explorar.
En un universo dominado por ceros y unos, las fracciones binarias representan un desafío intrigante: ¿es posible convertir cualquier fracción decimal a binario? La respuesta corta es no, pero hay mucho más detrás de esa negativa.
Aquí desglosamos lo esencial sobre las fracciones binarias:
- ¿Qué es una fracción binaria?: Una forma de representar números menores a uno en base 2.
- Conversión básica: Aprende a transformar una fracción decimal a su equivalente binario multiplicando por dos repetidamente.
- Limitaciones tecnológicas: Descubre cómo la capacidad finita de memoria afecta la precisión en representaciones numéricas.
- Errores inevitables: No todas las fracciones decimales tienen una representación binaria exacta; el error depende del número de dígitos utilizados.
- Uso práctico: Con nuestra herramienta convertidora, verás lo sencillo que puede ser manejar estas conversiones.
Sumérgete con nosotros en este tema complejo pero apasionante y descubre cómo estas pequeñas cifras controlan gran parte del mundo digital que nos rodea. ¡Te prometemos que será un viaje revelador!
Representación binaria
La representación binaria es fundamental en el mundo de la informática. Utiliza solo dos dígitos: 0 y 1, lo que la hace ideal para sistemas digitales. Cada posición en un número binario representa una potencia de 2. Por ejemplo, en el número binario 101, el dígito más a la derecha representa (2^0), el siguiente (2^1), y así sucesivamente. Esta estructura permite que las computadoras realicen cálculos de manera eficiente.
Pero, ¿cómo se relaciona esto con las fracciones? Las fracciones binarias funcionan de manera similar a las decimales, pero en lugar de dividir por 10, cada posición a la derecha del punto binario divide por 2. Esto permite representar números fraccionarios en un sistema que solo entiende ceros y unos.
Las fracciones binarias son esenciales en la programación y el diseño de hardware, ya que facilitan la manipulación de datos en formatos que las máquinas pueden procesar rápidamente.
¿Qué es una fracción binaria?
Una fracción binaria es la parte fraccionaria de un número expresada en base 2. Se deriva de la fracción decimal, que generalmente tiene un denominador que es una potencia de diez. En el caso binario, se utilizan potencias negativas de dos. Por ejemplo, 0.1 en binario equivale a 1/2 en decimal.
Convertir una fracción decimal a binaria implica multiplicar la parte decimal por 2 y registrar los resultados enteros hasta alcanzar la precisión deseada o que la parte fraccionaria se convierta en cero. Sin embargo, no todas las fracciones decimales pueden representarse perfectamente en binario.
Solo aquellas con denominadores que son potencias de dos tienen representaciones exactas. Por ejemplo, 1/2 se representa como 0.1 en binario, mientras que fracciones como 1/3 resultan en una representación binaria infinita, lo que lleva a errores de conversión.
Cómo convertir fracciones a binario
La conversión de fracciones decimales a binario puede parecer complicada, pero con un método paso a paso, se vuelve más sencilla. Aquí te mostramos cómo hacerlo:
- Multiplica la parte fraccionaria por 2: Si el resultado es mayor o igual a 1, anota un 1 y resta 1 del resultado.
- Continúa con la nueva fracción: Repite el proceso hasta que la fracción se convierta en 0 o hasta que obtengas el número de dígitos deseados.
- Registra los resultados: Cada número entero obtenido se convierte en un dígito en la representación binaria.
Por ejemplo, para convertir 0.625 a binario, multiplica 0.625 por 2 para obtener 1.25. Anota el 1 y continúa con 0.25. Repite hasta obtener la secuencia binaria completa.
La conversión de fracción binaria a fracción decimal
Para convertir una fracción binaria a decimal, sigue estos pasos:
- Identifica cada posición: Cada dígito después del punto binario representa una potencia negativa de 2.
- Multiplica y suma: Multiplica cada dígito por su potencia correspondiente y suma los resultados.
Por ejemplo, para convertir 0.101 en decimal, calcula ( (1 \times 2^-1) + (0 \times 2^-2) + (1 \times 2^-3) ), lo que da como resultado 0.625.
Ejemplos comunes de fracciones binarias y sus conversiones
Aquí te presentamos algunos ejemplos comunes de fracciones binarias y sus equivalentes decimales:
| Fracción Binaria | Fracción Decimal |
|---|---|
| 0.1 | 0.5 |
| 0.01 | 0.25 |
| 0.11 | 0.75 |
| 0.101 | 0.625 |
Las limitaciones de las fracciones binarias
Las fracciones binarias, aunque útiles, tienen limitaciones. No todas las fracciones decimales se pueden representar exactamente en binario. Esto se debe a que algunas fracciones, como 1/3, tienen representaciones binarias infinitas.
Además, los sistemas informáticos tienen una capacidad limitada para almacenar dígitos, lo que puede llevar a errores de redondeo. Estos errores pueden afectar la precisión de cálculos en aplicaciones científicas y financieras.
Por ejemplo, la fracción 1/10 no se puede representar exactamente en binario, lo que puede causar problemas en cálculos precisos.
¿Cómo usar nuestro convertidor de fracciones binarias?
Usar un convertidor de fracciones binarias es sencillo. Aquí te explicamos cómo:
- Selecciona el tipo de conversión: Decide si vas a convertir de decimal a binario o viceversa.
- Introduce el número: Ingresa la fracción decimal o binaria que deseas convertir.
- Obtén el resultado: El convertidor te dará la representación equivalente en la otra base.
Para convertir una fracción decimal a binario, sigue multiplicando la parte decimal por 2, registrando los enteros obtenidos. Para convertir de binario a decimal, multiplica cada dígito por su potencia de 2 correspondiente y suma los resultados.
Aplicaciones de fracciones binarias en informática y tecnología
Las fracciones binarias son cruciales en la informática y la tecnología. Permiten representar valores no enteros en sistemas digitales, lo que es esencial para cálculos precisos.
En las computadoras, las fracciones binarias se utilizan en operaciones de punto flotante, que son fundamentales para manejar números muy grandes o pequeños. Estas operaciones son vitales en aplicaciones científicas, financieras y de ingeniería.
Sin embargo, debido a la precisión limitada de las fracciones binarias, pueden ocurrir errores de redondeo. Para mitigar estos errores, se emplean técnicas como la representación de mayor precisión y corrección de errores.
Más allá de 0s y 1s
Las fracciones binarias no solo representan ceros y unos. Permiten expresar cantidades de manera precisa, similar a las fracciones decimales. Cada posición en una fracción binaria corresponde a potencias negativas de dos, lo que permite representar valores fraccionarios.
Además, las fracciones binarias son esenciales para interpretar formatos de datos como el estándar IEEE 754, utilizado para la aritmética de punto flotante. Este estándar mejora la eficiencia computacional y es crucial en la arquitectura de computadoras.
Preguntas Frecuentes
¿Se pueden convertir todas las fracciones a binario?
No, no todas las fracciones se pueden representar exactamente en binario. Solo las fracciones con denominadores que son potencias de dos tienen representaciones finitas. Las demás pueden resultar en representaciones infinitas o aproximadas.
¿Cómo convertir fracciones a binario?
Para convertir fracciones decimales a binario, multiplica la parte decimal por 2. Anota el entero y repite hasta alcanzar la precisión deseada o que la fracción sea cero.
¿Cómo se representa 0.5 en binario?
El número 0.5 se representa en binario como 0.1. Esto se debe a que 0.5 equivale a 1/2, que es (2^-1).
¿Qué es 0.1101 en decimal?
Para convertir 0.1101 a decimal, suma las potencias de dos correspondientes: ( (1 \times 2^-1) + (1 \times 2^-2) + (0 \times 2^-3) + (1 \times 2^-4) ), lo que resulta en 0.8125.
Conclusion
El mundo de las fracciones binarias es un fascinante rompecabezas en el ámbito digital, donde cada pieza encaja para permitir que las computadoras procesen números no enteros. Aunque no todas las fracciones decimales pueden convertirse perfectamente a binario, este desafío técnico resalta la belleza de la matemática aplicada a la tecnología. Comprender cómo estas conversiones se realizan nos abre una ventana al funcionamiento interno de los sistemas digitales.
Las fracciones binarias son esenciales para representar valores fraccionarios en una base que solo conoce ceros y unos, haciendo posible cálculos precisos en campos como la programación y el diseño de hardware. Sin embargo, enfrentamos limitaciones debido a la capacidad finita de memoria y los inevitables errores de redondeo que pueden surgir.
A través del uso práctico de herramientas como nuestro convertidor de fracciones binarias, podemos simplificar estos procesos complejos y hacerlos accesibles para cualquier interesado en profundizar su comprensión del tema. En última instancia, estas pequeñas cifras binarias son los engranajes invisibles que impulsan gran parte del mundo digital moderno. A medida que exploramos más sobre ellas, descubrimos cómo controlan aspectos cruciales de nuestra vida tecnológica diaria.